Lectures
Lecture, help sessions and grading sessions information
There is a menu item for each lecture where you can find a reading guide for the textbook, and links to additional material.
Please note that this timetable is still preliminary and is subject to change. The official timetable is in timeedit.
For the lecture locations please look at timeedit timeedit schedule is always correct. If there are any discrepancies between this page and timeedit, then please inform me.
| Lecture/Assignment | Date | Topic |
|---|---|---|
| 1 | 2025-11-10 13-15 | Introduction to the course and revision of Algorithm analysis |
| 2 | 2025-11-13 15-17 | Revision of Graphs, and the Python API for the assignments (Frej Knutar Lewander) |
| 3 | 2025-11-14 10-15 | Dynamic Programming - Introduction |
| Help 1a | 2025-11-14 13-15 | |
| 4 | 2025-11-17 13-15 | Dynamic Programming - Knapsack |
| Help 1b | 2025-11-19 15-17 | |
| Help 1c | 2025-11-20 13-17 | |
| 5 | Greedy Algorithms | |
| Deadline Assignment 1 | 2025-11-25 15:00 | |
| 6 | Minimal Spanning Trees | |
| Help 2a | 2025-11-16 10-12 | |
| Grading session Assignment 1 | TBA | By invitation only |
| 7 | 2025-12-01 10-12 | Network flows |
| Help 2b | 2025-12-01 13-15 | |
| Solution Session Assignment 1 | 2025-12-04 09-10 | Obs only 45 mins |
| 8 | 2025-12-04 13-15 | Networks flows, Bipartite matching |
| Help 2c | 2025-12-03 08-10 | |
| Deadline Assignment 2 | 2025-12-05 15:00 | |
| 9 | 2025-12-08 10-12 | Union Find |
| Help 3a | 2025-12-09 13-15 | |
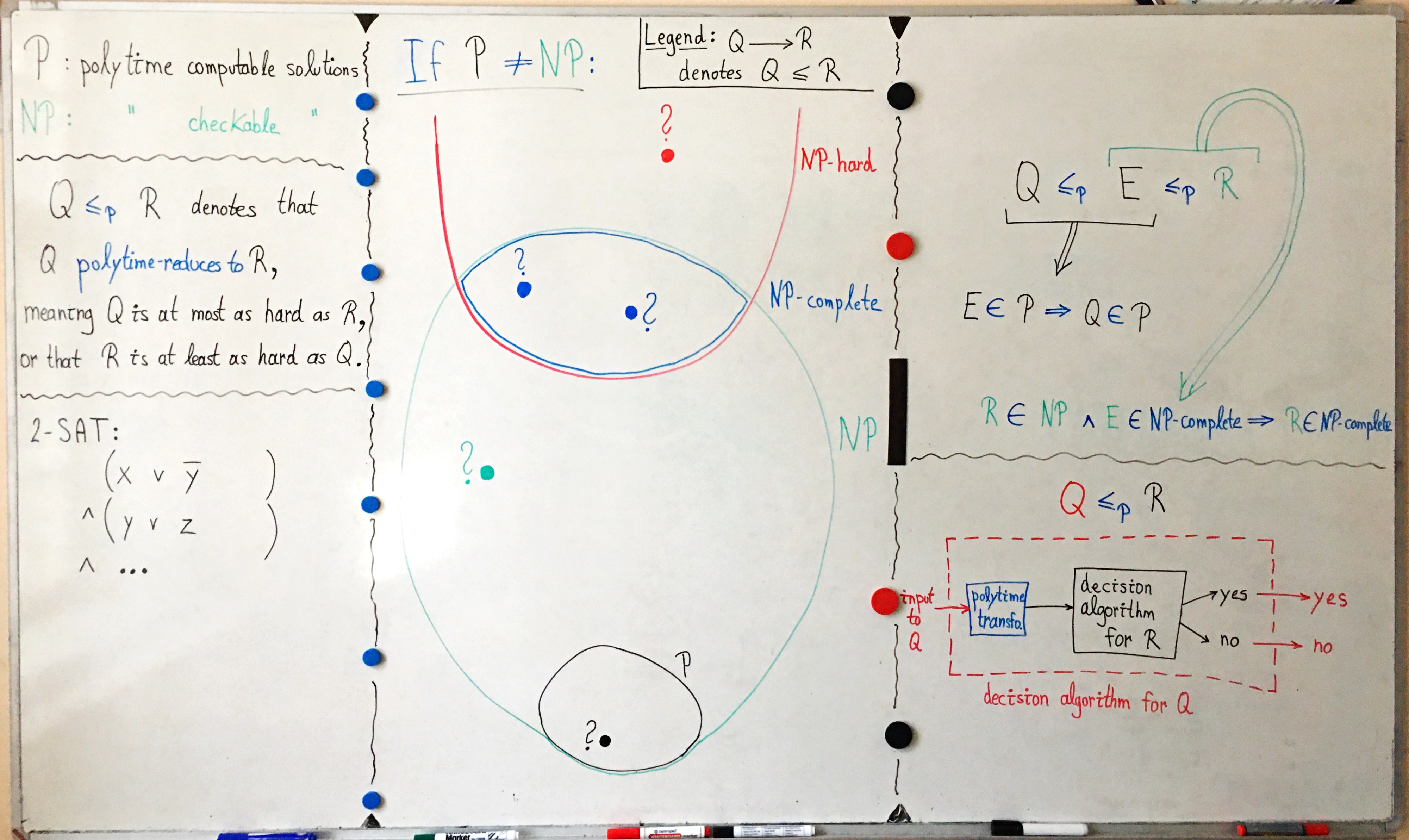
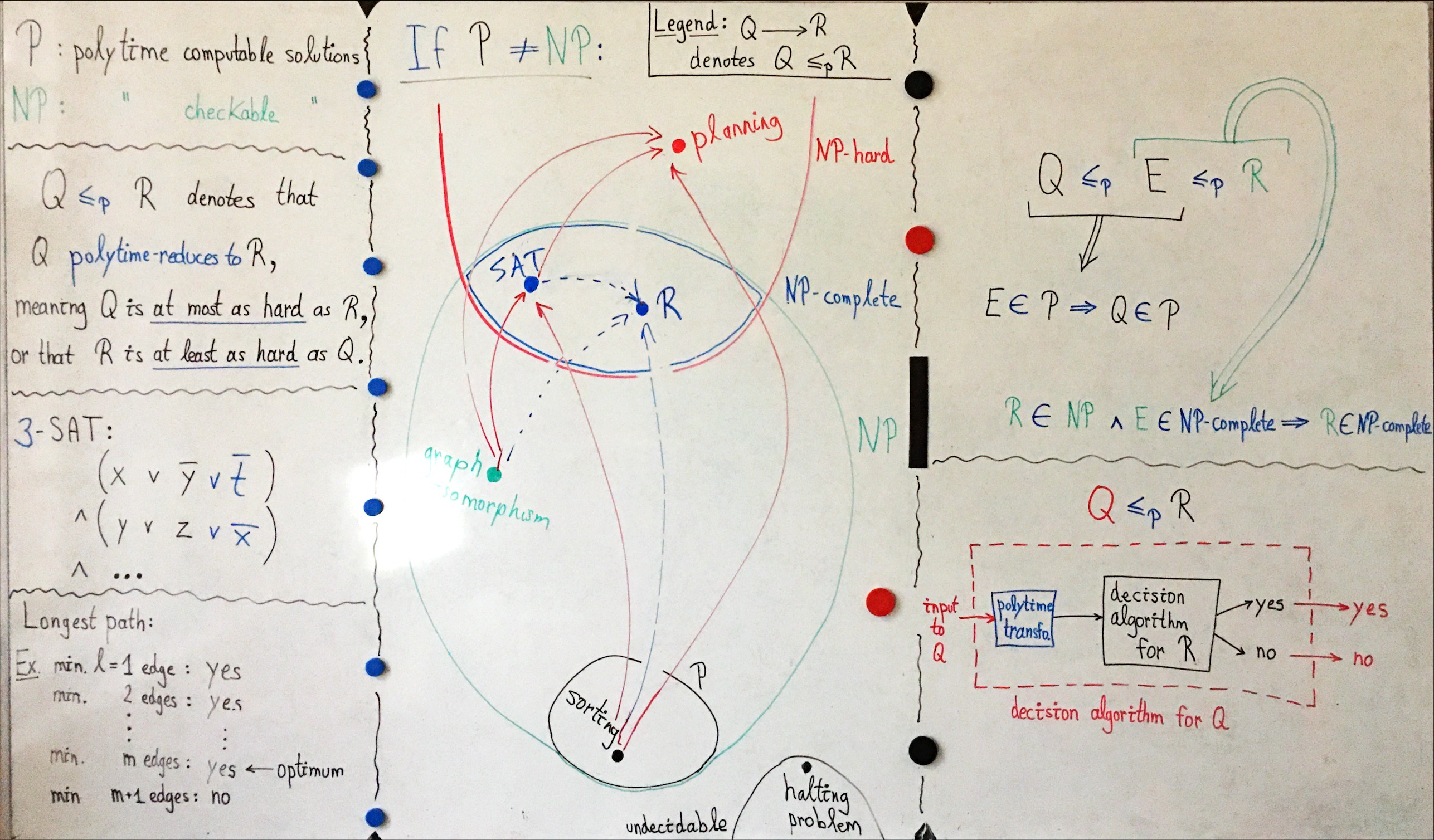
| 10 | 2025-12-11 | P vs NP (Pierre Flener) |
| Help 3b | 2025-12-12 15-17 | |
| 11 | 2025-12-15 | P vs NP (Pierre Flener) |
| Solution Session Assignment 2 | 2015-12-15 15-16 | Obs only 45 mins |
| Help 3c | 2025-12-18 15-17 | |
| Exam | 2025-01-05 | TBA |
| Deadline Assignment 3 | 2026-01-09 15:00 |